Resolving kinematic collisions

Using kinematic collision objects require you to resolve collisions yourself and move the objects as a reaction. A naive implementation of separating two colliding objects looks like this:

function on_message(self, message_id, message, sender)
  -- Handle collision
  if message_id == hash("contact_point_response") then
    local newpos = go.get_position() + message.normal * message.distance
    go.set_position(newpos)
  end
end

This code will separate your kinematic object from other physics object it penetrates, but the separation often overshoots and you will see jitter in many cases. To understand the problem better, consider the following case where a player character has collided with two objects, A and B:

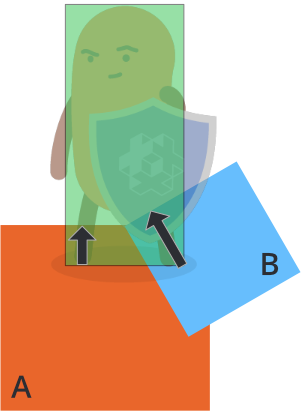
The physics engine will send multiple "contact_point_response" message, one for object A and one for object B the frame the collision occurs. If you move the character in response to each penetration, as in the naive code above, the resulting separation would be:

• Move the character out of object A according to its penetration distance (the black arrow)
• Move the character out of object B according to its penetration distance (the black arrow)

The order of these is arbitrary but the result is the same either way: a total separation that is the sum of the individual penetration vectors:

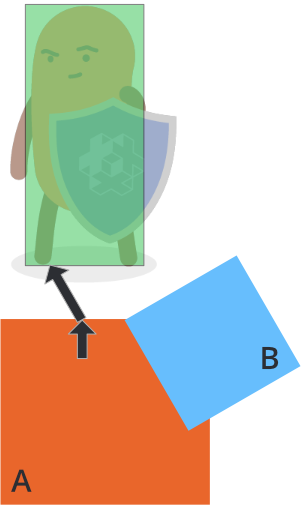
To properly separate the character from objects A and B, you need to handle each contact point’s penetration distance and check if any previous separations have already, wholly or partially, solved the separation.

Suppose that the first contact point message comes from object A and that you move the character out by A’s penetration vector:

Then the character has already been partially separated from B. The final compensation necessary to perform full separation from object B is indicated by the black arrow above. The length of the compensation vector can be calculated by projecting the penetration vector of A onto the penetration vector of B:

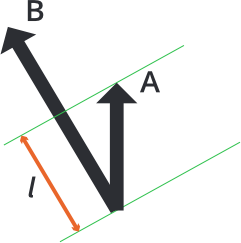
l = vmath.project(A, B) * vmath.length(B)

The compensation vector can be found by reducing the length of B by l. To calculate this for an arbitrary number of penetrations, you can accumulate the necessary correction in a vector by, for each contact point, and starting with a zero length correction vector:

1. Project the current correction against the contact’s penetration vector.
2. Calculate what compensation is left from the penetration vector (as per the formula above).
3. Move the object by the compensation vector.
4. Add the compensation to the accumulated correction.

A complete implementation looks like this:

function init(self)
  -- correction vector
  self.correction = vmath.vector3()
end

function update(self, dt)
  -- reset correction
  self.correction = vmath.vector3()
end

function on_message(self, message_id, message, sender)
  -- Handle collision
  if message_id == hash("contact_point_response") then
    -- Get the info needed to move out of collision. We might
    -- get several contact points back and have to calculate
    -- how to move out of all of them by accumulating a
    -- correction vector for this frame:
    if message.distance > 0 then
      -- First, project the accumulated correction onto
      -- the penetration vector
      local proj = vmath.project(self.correction, message.normal * message.distance)
      if proj < 1 then
        -- Only care for projections that does not overshoot.
        local comp = (message.distance - message.distance * proj) * message.normal
        -- Apply compensation
        go.set_position(go.get_position() + comp)
        -- Accumulate correction done
        self.correction = self.correction + comp
      end
    end
  end
end