Read this manual in English

Rozwiązywanie kolizji kinematycznych

Korzystanie z kinematycznych obiektów kolizji (kinematic collision objects) wymaga się od Ciebie ręcznego rozwiązywania kolizji i przemieszczania obiektów jako reakcji na nie. Proste podejście do rozdzielenia dwóch kolidujących obiektów wygląda następująco:

function on_message(self, message_id, message, sender)
  -- Handle collision
  if message_id == hash("contact_point_response") then
    local newpos = go.get_position() + message.normal * message.distance
    go.set_position(newpos)
  end
end

Ten kod rozdzieli Twój obiekt kinematyczny od innych obiektów fizycznych, które penetruje, ale rozdzielenie często jest zbyt duże, co prowadzi do drgań w wielu przypadkach. Aby lepiej zrozumieć problem, rozważmy następujący przypadek, w którym postać gracza koliduje z dwoma obiektami, A i B:

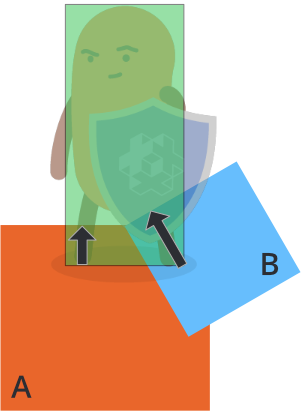
Silnik fizyki wyśle wiele wiadomości "contact_point_response", jedną dla obiektu A i jedną dla obiektu B w klatce, w której wystąpiła kolizja. Jeśli przesuniesz postać w odpowiedzi na każde przeniknięcie, jak w prostym kodzie powyżej, to rozdzielenie będzie się prezentować następująco:

• Przesuń postać poza obiekt A zgodnie z jego odległością penetracji (czarna strzałka).
• Przesuń postać poza obiekt B zgodnie z jego odległością penetracji (czarna strzałka).

Kolejność tych działań jest dowolna, ale wynik jest taki sam w obu przypadkach: całkowite rozdzielenie, które stanowi sumę wektorów penetracji poszczególnych obiektów:

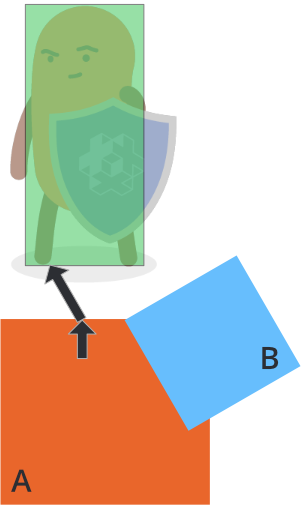
Aby właściwie rozdzielić postać od obiektów A i B, musisz obsłużyć odległość penetracji punktów kontaktowych i sprawdzić, czy jakiekolwiek wcześniejsze rozdzielenia już całkowicie lub częściowo rozwiązały problem rozdzielenia.

Załóżmy, że pierwsza wiadomość punktu kontaktowego pochodzi od obiektu A i przesuwasz postać poza obiekt A zgodnie z wektorem penetracji A:

Wtedy postać zostaje już częściowo rozdzielona od obiektu B. Ostateczna korekta konieczna do pełnego rozdzielenia od obiektu B jest wskazana czarną strzałką powyżej. Długość wektora kompensacji (compensation vector) można obliczyć, projektując wektor penetracji A na wektor penetracji B:

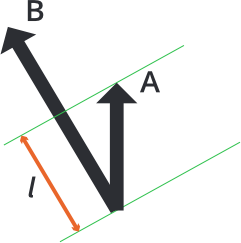
l = vmath.project(A, B) * vmath.length(B)

Wektor kompensacji można znaleźć, zmniejszając długość B o l. Aby obliczyć to dla dowolnej liczby penetracji, można akumulować niezbędną korektę w wektorze, który zaczyna się od wektora kompensacji o zerowej długości:

1. Zweryfikuj projekcję bieżącej korekcji na wektor penetracji kontaktu.
2. Oblicz, ile kompensacji pozostało z wektora penetracji (zgodnie z powyższym wzorem).
3. Przesuń obiekt o wektor kompensacji.
4. Dodaj kompensację do akumulowanej korekty.

Pełna implementacja wygląda tak:

function init(self)
  -- wektor korekcji (kompensacji)
  self.correction = vmath.vector3()
end

function update(self, dt)
  -- zresetuj wektor korekcji
  self.correction = vmath.vector3()
end

function on_message(self, message_id, message, sender)
  -- Obsługa kolizji
  if message_id == hash("contact_point_response") then
    -- Pobierz informacje potrzebne do rozdzielenia kolizji. Możemy
    -- otrzymać wiele punktów kontaktowych i musimy obliczyć,
    -- jak się z nich wycofać, akumulując korekcję
    -- na tę klatkę:
    if message.distance > 0 then
      -- Po pierwsze, zweryfikuj projektowaną korekcję na
      -- wektor penetracji akumulowany
      local proj = vmath.project(self.correction, message.normal * message.distance)
      if proj < 1 then
        -- Weź pod uwagę tylko projekcje, które nie przestrzeliły.
        local comp = (message.distance - message.distance * proj) * message.normal
        -- Dodaj kompensację
        go.set_position(go.get_position() + comp)
        -- Akumuluj korekcję
        self.correction = self.correction + comp
      end
    end
  end
end